Aus drei Strecken mit den Längen a, b und c lässt sich genau dann ein Dreieck bilden, wenn sie die Dreiecksungleichung(en) erfüllen. Das bedeutet, dass jede Seite kürzer sein muss als die beiden übrigen Seiten zusammen, also

a < b+c,\\ b < a+c \text{ und}\\ c < a+b.

Die Wahrscheinlichkeit dafür, dass sich aus den drei Bruchstücken der Spaghetti ein Dreieck legen lässt, beträgt \frac{1}{4}.

Der Einfachheit halber normieren wir die Länge einer Spaghetti auf 1. Für die drei Stücke a, b und c gilt dann also a+b+c=1.


Zur Dreiecksungleichung:

Es gibt mehrere Möglichkeiten, dieses Ergebnis zu erhalten. Alle Lösungswege basieren auf der Einhaltung der Dreiecksungleichung (siehe Hinweis).

Die Dreiecksungleichung ist automatisch erfüllt, solange keines der drei Stücke die Länge \frac{1}{2} oder größer hat.

Ist eine Seite (z. B. a) nämlich kürzer als \frac{1}{2}, dann sind die beiden übrigen Stücke zusammen länger als \frac{1}{2} und damit länger als a, wie gewünscht.

Sind sogar alle drei Seiten kürzer als \frac{1}{2}, sind die drei Dreiecksungleichungen erfüllt und es kann ein Dreieck gebildet werden.



Wie groß ist also die Wahrscheinlichkeit, dass alle Stücke kürzer sind als \frac{1}{2}?

Dazu erstellen wir ein Diagramm, in dem wir alle möglichen Fälle klassifizieren, wie die Spaghetti in drei Teile zerbrechen kann. Ein zufälliger Bruch an zwei Stellen entspricht genau einem Punkt in diesem Diagramm.

Dabei beschreibt die x-Achse die Position der 1. Bruchstelle und die y-Achse die Position der 2. Bruchstelle (jeweils gemessen vom linken Ende der Spaghetti).

Damit ergibt sich folgendes Diagramm:




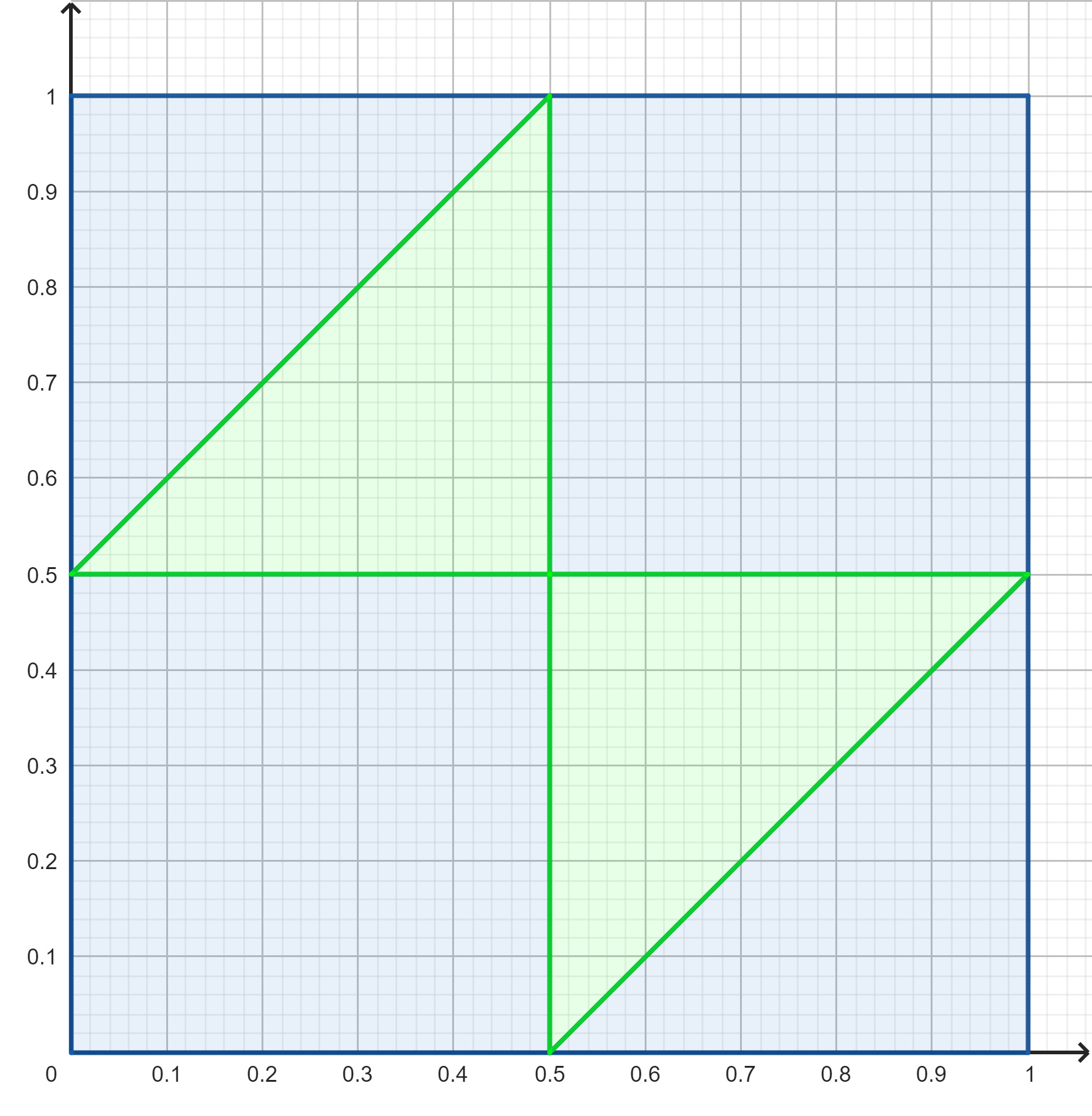
Bei allen Fällen im blauen Bereich lässt sich kein Dreieck legen, da dort eines der Bruchstücke länger ist als \frac{1}{2}. Wir analysieren die einzelnen Bereiche.

1. Quadrat unten links:
Hier liegen beide Bruchstellen links der Mitte. Somit ist das dritte Stück (von links) länger als die Hälfte.

2. Quadrat oben rechts: (Symmetrisch zu 1.)
Hier sind beide Bruchstellen auf der rechten Seite. Somit ist das erste Stück (von links) länger als die Hälfte der Spaghetti.

3. Dreieck oben links:
Die erste Bruchstelle ist links der Mitte, die zweite Bruchstelle mehr als 0,5 weiter rechts. Damit ist das Mittelstück länger als \frac{1}{2}.

4. Dreieck unten rechts: (Symmetrisch zu 4.)
Die erste Bruchstelle ist rechts der Mitte, die zweite Bruchstelle mehr als 0,5 weiter links. Damit ist das Mittelstück länger als \frac{1}{2}.


Grüne Dreiecke
Für jeden Punkt in den beiden grünen Dreiecken ist der Abstand seiner x- und y-Koordinate kleiner als 0,5. Damit ist also der Abstand der Bruchstellen kleiner als 0,5 und ein Dreieck kann aus den Bruchstücken gebildet werden.


Die Wahrscheinlichkeit ergibt sich dann als Anteil der grünen Fläche an der Gesamtfläche. Dieser entspricht offensichtlich genau einem Viertel.